Indholdsoversigt
- Snit i brædder og lister
- Halve vinkler giver pæne hjørner
- Store afstande kræver store vinkler
- Præcist arbejde med ukendte mål
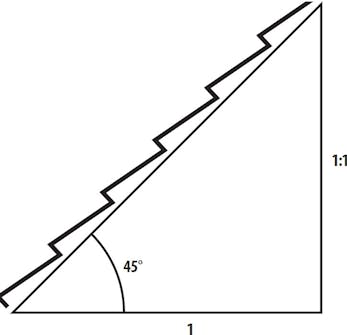
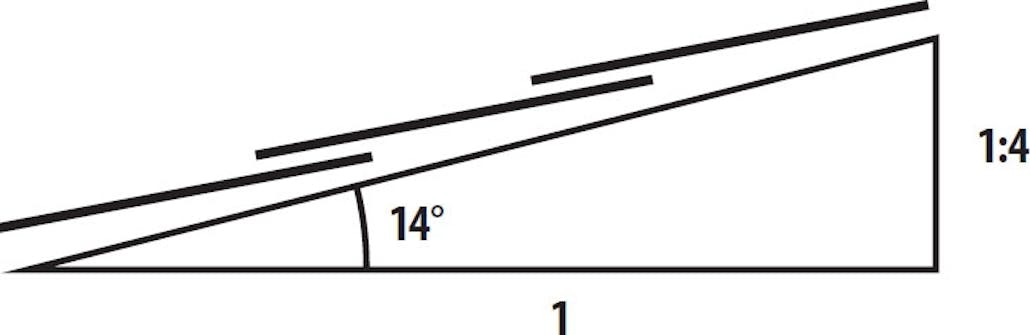
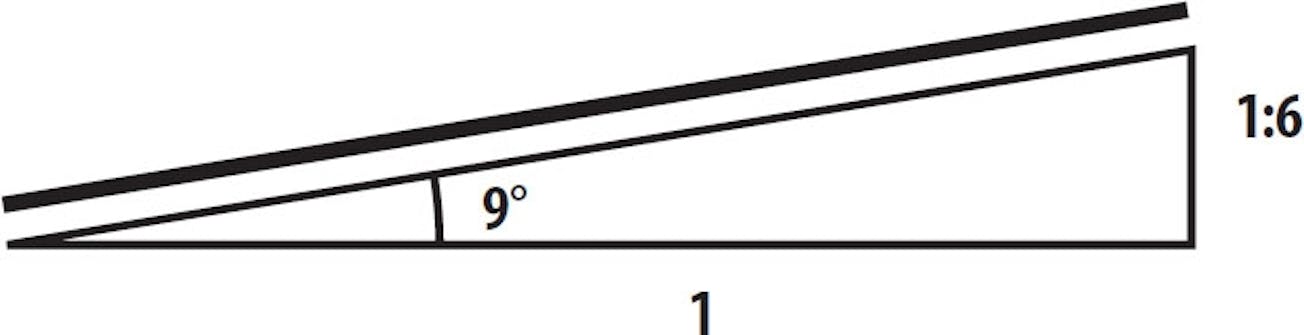
- Brug forholdstal - når terrassen skal have fald
- Find tagets hælding
- Tagrendens fald måles i promiller
- Perfekt vinkel til arbejde over store afstande
- VIDEO: Vinkel til større projekter
Snit i brædder og lister
90 grader kendes også som en ret vinkel. Den er så almindelig, at vi sjældent tænker på den som 90 grader.
45 grader er langt det mest almindelige skrå snit. To stykker træ skåret på 45 grader kan nemlig samles i en ret vinkel (= 90 grader).
60 grader finder du i hjørnerne på en trekant med lige lange sider, og 60 grader deler cirklen i 6 lige store stykker.
To 30 graders snitsamles til et hjørne på 60 grader, men oftest bruger du, at 30 plus 60 grader bliver til 90 grader.
Halve vinkler giver pæne hjørner
Store afstande kræver store vinkler
Præcist arbejde med ukendte mål
Brug forholdstal - når terrassen skal have fald
Først mærkes samme højde op på en pind i hver ende af belægningen. Start med den ende, hvor faldet skal “løbe væk” fra ...
Find tagets hælding
Tagrendens fald måles i promiller
Perfekt vinkel til arbejde over store afstande
VIDEO: Vinkel til større projekter
Den laver du nemt selv af tre brædder